定幅曲線

定幅曲線とはどの方向から測っても幅が一定の凸閉曲線です。
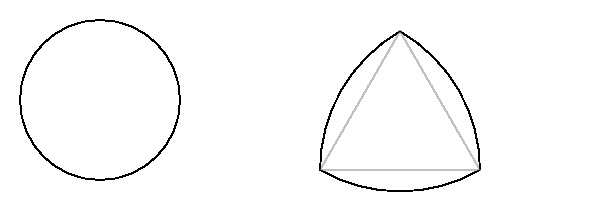
円の他に有名な例として、 ルーローの三角形(下右図, 正三角形の各頂点を中心に他の２つの頂点を結ぶ円弧を描いてできる)があります。


次の定理は中学校までに習う数学の範囲で証明できます。

定理 1　 C を定幅曲線とし、Cを平行な二直線 l と m で はさんだときの l と C の接点、 m と C の接点をそれぞれ A、B とすれば、
AB と l は直交する。

上の定理により定幅曲線は半分の形から残り半分の形が決まることがわかります。
上半分が　 x = cos(t), y = * sin(t) 　(0 < t < π)　で表される楕円の定幅曲線

上の入力ボックスに 0.4 ぐらいの数値を入れて上半分を再描画してから下半分を描画する様子を 観察することにより、
半径が幅の円より緩やかな曲りぐあいの定幅曲線はないことがわかります。
また、上の定理より、幅が d の定幅曲線の一部分が半径 r の円弧ならば、 r ≦ d であり、反対側は半径 d-r の円弧になります。

定理 2　 閉区間 [0, 2π] で定義された C1 級の関数　h(θ) が 次の (1), (2), (3) をみたせば
　　　x = (cos θ)h(θ) - (sin θ)h'(θ)
　　　y = (sin θ)h(θ) + (cos θ)h'(θ)
で表される曲線は幅が d の定幅曲線である。
(1) 0 ≦ θ ≦ π に対して h(θ) + h(θ + π) = d
(2) h(θ) は区分的に C2級
(3) h''(θ) が定義されている所で 0 ≦ h(θ) + h''(θ) ≦ d

上の定理の h(θ) + h''(θ) は曲線の曲率半径 (曲率の逆数、同じ半径の円と同じ曲がりぐあい)です。
正の実数 r と実数 a, b により ある区間で h(θ) = r + a cos θ + b sin θ ならば、上の定理の曲線の一部は中心が (a, b) で半径が r の円弧となります。 また、同じ区間で h(θ) + h''(θ) = r で定数となります。

Type I:(d=2) h(t) = 1+ cos(3t) +sin(5t) , 　, 　, 　, 　


Type II : 1. < b = < √2, t0 = π / b.
h(θ) = 1 + cos(bθ)　 for 0 < θ < t0
h(θ) = 0 　　　　　　for t0 < θ < π

Type III :
h(θ) = 4(θ - π / 2)2 / π2　 for 0 < θ < π

Type IV : tan t0 = 0.75.
h(θ) = 1.75 - cos(θ) 　　　for 0 < θ < t0
h(θ) = 0.5 + 0.75 * sin(θ) 　for t0 < θ < π/2
h(θ) = 1.25　　　　　　　　for π/2 < θ < π

Type V : (c は 0 < c < π/2, (π/2 - c)tan(1.5c - π) = 2/3 を満たす実数)
h(θ) = 1 + 0.8 cos(1.5 θ - π) 　　　for 0 < θ < c
h(θ) = 1 + 1.2 (θ - π/2) sin(1.5 c) 　for c < θ < π - c
h(θ) = 1 + 0.8 cos(1.5 (θ - π)) 　　　for π - c < θ < π