Curves of constant width

A curve of constant width is a closed curve C
such that the distance of the two parallel lines which catch C
does not depend the slope.
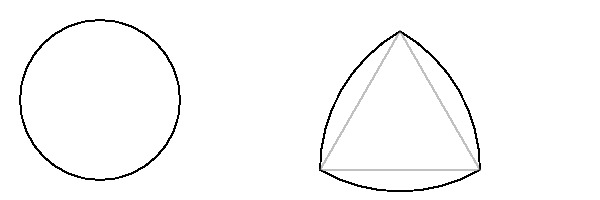
Circles and Rulos triangles are typical examples of curves of constant width

Theorem 1
Let C be a curve of constant width.
If we catch C by two parallel lines,
then each line contacts with C at one point
and the line connecting the two contact points is orthogonal to the two lines.

The curve of constant width whose upper half is expressed by
x = cos(t), y = * sin(t) 　(0 < t < π).


Theorem 2
If a C¹class function h(θ) on [0, 2π] satisfies the following condtions (i), (ii) and (iii), then the curve defined by
　x = (cos θ)h(θ) - (sin θ)h'(θ),　 　y = (sin θ)h(θ) + (cos θ)h'(θ)
is of constant width.
(i) h(θ) + h(θ + π) = d
(ii) h(θ) is C³ class except at finite points.
(iii) 0 ≦ h(θ) + h''(θ) ≦ d

If h(θ) = r + a cos θ + b sin θ on an interval,
then a part of the curve in the above theorem is a circular arc with a radius of r and the center (a, b).

Type I : (d=2) h(θ) = 1+ cos(3θ) +sin(5θ) , 　, 　, 　, 　

Then the blue curve go around once in the above square box.

Type II : 1. < b = < √2, t0 = π / b.
h(θ) = 1 + cos(bθ)　 for 0 < θ < t0
h(θ) = 0 　　　　　　for t0 < θ < π

Type III :
h(θ) = 4(θ - π / 2)² / π²　 for 0 < θ < π

Type IV : tan t0 = 0.75.
h(θ) = 1.75 - cos(θ) 　　　for 0 < θ < t0
h(θ) = 0.5 + 0.75 * sin(θ) 　for t0 < θ < π/2
h(θ) = 1.25　　　　　　　　for π/2 < θ < π

Type V : (c is a real number satisfying 0 < c < π/2 and (π/2 - c)tan(1.5c - π) = 2/3.)
h(θ) = 1 + 0.8 cos(1.5 θ - π) for 0 < θ < c
h(θ) = 1 + 1.2 (θ - π/2) sin(1.5 c) for c < θ < π - c
h(θ) = 1 + 0.8 cos(1.5 (θ - π)) for π - c < θ < π