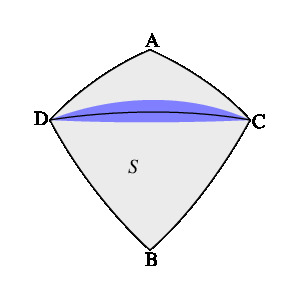
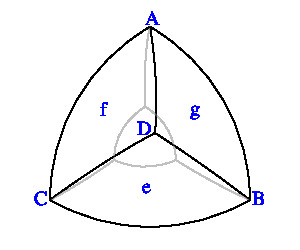
 同じ操作を ABD と CBD, ABC と DBC に対して行う。
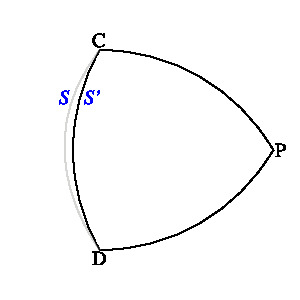
このようにして得られた曲面を S' とする。
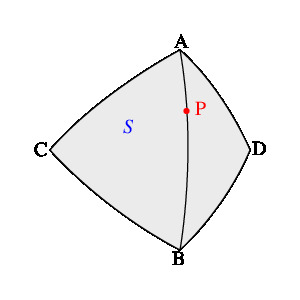
P を C, D を中心とし半径 1 の球面の交わりの S 上の任意の点とするとき
(上中央の図)、
平面 PCD と S' の交わりはルーローの三角形であるから、
PCD に直交し、S' を挟む平行な 2平面の間の距離は 1 である。
したがって、S' は定幅曲面である。
以下で、定義する自己双対球面多面体に対して
上で S に対して行ったのと同じ操作を行えば、
定幅曲面が得られる。
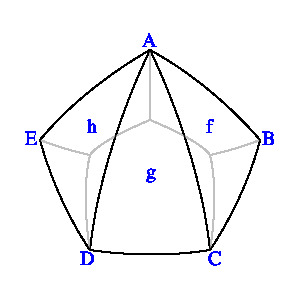
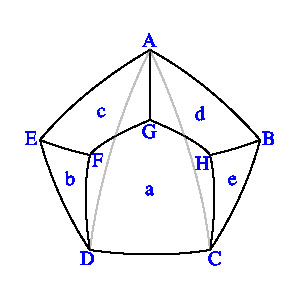
定義 各面が半径 1 の球面の一部分である
多面体 P の頂点の個数と面の個数が等しく、
頂点の集合から面の集合への一対一写像 f があり、
以下の条件 (i), (ii), (iii) を満たすとき、P を
同じ操作を ABD と CBD, ABC と DBC に対して行う。
このようにして得られた曲面を S' とする。
P を C, D を中心とし半径 1 の球面の交わりの S 上の任意の点とするとき
(上中央の図)、
平面 PCD と S' の交わりはルーローの三角形であるから、
PCD に直交し、S' を挟む平行な 2平面の間の距離は 1 である。
したがって、S' は定幅曲面である。
以下で、定義する自己双対球面多面体に対して
上で S に対して行ったのと同じ操作を行えば、
定幅曲面が得られる。
定義 各面が半径 1 の球面の一部分である
多面体 P の頂点の個数と面の個数が等しく、
頂点の集合から面の集合への一対一写像 f があり、
以下の条件 (i), (ii), (iii) を満たすとき、P を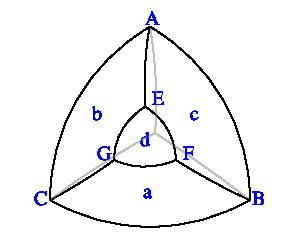
 最後に、回転体でもなく、
自己双対球面多面体からも得られない定幅曲面の例(幅は 2)を示す。
下の図形は定幅曲線である。
この図形を以下のように動かしたときの軌跡が定福曲面となる。
直線 OP1 を軸に P2 が
P3 に重なるように 90度回転し、
回転後の図形を直線 OP3 を軸に P1 が
P2 に重なるように 90度回転し、
さらに、直線 OP2 を軸に P3 が
P1 に重なるように 90度回転する。
最後に、回転体でもなく、
自己双対球面多面体からも得られない定幅曲面の例(幅は 2)を示す。
下の図形は定幅曲線である。
この図形を以下のように動かしたときの軌跡が定福曲面となる。
直線 OP1 を軸に P2 が
P3 に重なるように 90度回転し、
回転後の図形を直線 OP3 を軸に P1 が
P2 に重なるように 90度回転し、
さらに、直線 OP2 を軸に P3 が
P1 に重なるように 90度回転する。
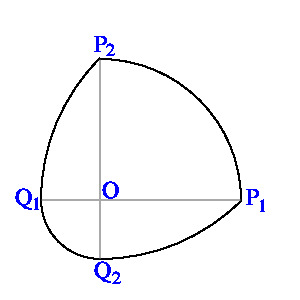
P1 = (√2, 0, 0),
P2 = (0, √2, 0),
P3 = (0, 0, √2),
Q1 = (√2 - 2, 0, 0),
Q2 = (0, √2 - 2, 0),
Q3 = (0, 0, √2 - 2)
円弧 P1P2 : 中心 O, 半径 √2
円弧 P2Q1 : 中心 P1, 半径 2
円弧 Q1Q2 : 中心 O, 半径 2 - √2
円弧 Q2P1 : 中心 P2, 半径 2