双曲平面上のモンジュの定理
双曲平面上でもモンジュの定理は成り立ちます。
下図の円は円の中心をマウス(または指)で動かせます。
円の中心を大きい円(ポアンカレ円盤)の外に出せば円が等距離曲線に変わります。

1の半径 : 1.4,　 2の半径 : 0.25,　 3の半径 : 0.5

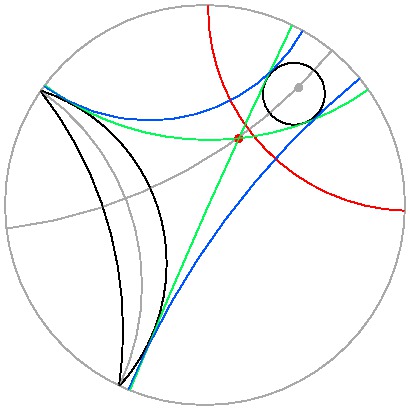
2つの円または等距離曲線が左下図のように 互いの外部にあるときまたは 4点で交わるときには 両方に接する4本の直線が引ける。
その 4本の中の 2本づつから下図のようにして 2つの対象が定まる。

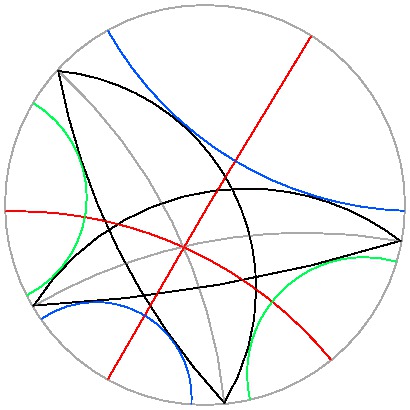
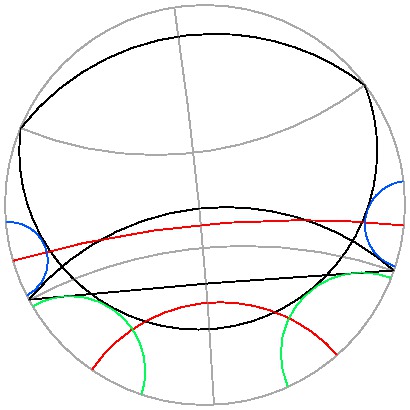
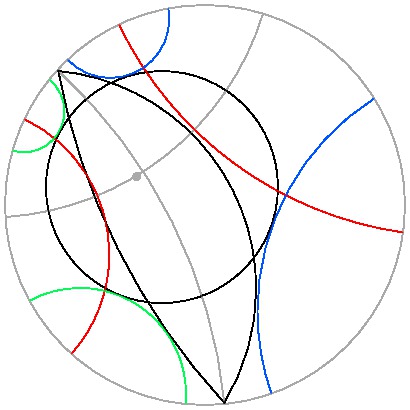
双曲平面上のモンジュの定理は次のように表現できる。
「3つの円または等距離曲線があり, どの2つに対しても 両方に接する直線が4本引けるとき, 4つの対象 P₁, P₂, P₃, P₄ があり, 上記のようにして定まる 6(=3x2) つの対象は P_iP_j (1 ≦ i < j ≦ 4) である。」