双曲平面上の幾何学


ここでは、双曲平面を Pascal の円盤モデルで考えることにします。
x2+y2=1 　 で表される円を　Γ、その内部を　Δ とします。
双曲平面の点とは　Δ 内の点であり、 双曲平面の直線とは　Γ の直径または Γ に直交する円の　Δ に含まれる部分です。
混乱を避けるためこれらを P点および P直線と呼ぶことにします。
簡単な計算により、P直線は a2+b2-4c2 > 0 をみたす実数 a, b, c により
ax + by + c(x2+y2+1) = 0
で表されることがわかります。 a2+b2-4c2 < 0 をみたす実数 a, b, c に対しては
以下のように P点を対応させ、 また、外積 * を定義します。

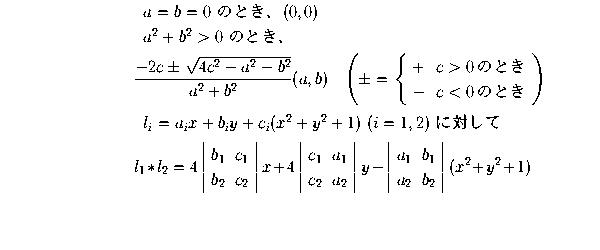
一見、不自然に思われるかもしれませんが、 このように定義すると話が非常にうまくいきます。
詳しくは 「双曲平面上の幾何学」（内田老鶴圃） を見て下さい。
l と m が P点を表すときは、 l * m はその二点を通る P直線を表し、
l と m が P直線を表すときは、 l * m はその二直線の交点または その両方に直交する P直線を表し、
l が P点を表し、 m が P直線を表すときは、 l * m は前者を通り、 後者に直交する P直線を表します。

下のボックス内の数値を変え、描画をクリックして試して下さい。


一番目のP点またはP直線 : A x+ y+ (x2+y2+1)
二番目のP点またはP直線 : B x+ y+ (x2+y2+1)
A 　を青、　 B 　を緑、　 A * B 　を赤で　 しています。
数値の目安
(x0, y0) を中心とし、Γに直交する円弧となるP直線は　　 (x0) x + (y0) y + (-0.5) (x2+y2+1)
(x0, y0) の位置のP点は　　　 (x0) x + (y0) y + (-0.25(x02+y02+1)) (x2+y2+1)

双曲平面上の三角形の垂心、外心、重心

以下で、l の表す P点または P直線を [l] で表すことにします。
l, m, n が P点を表すとき、 [l * (m * n)] は三角形[l][m][n] の頂点 [l] から対辺 [m * n] に下ろした垂線です。
双曲平面上の三角形の垂心 をクリックして試して下さい。
双曲平面上の三角形でも三本の垂線が1点で交わるか 三本のいずれとも直交する直線が存在することは
l * (m * n),　m * (n * l),　n * (l * m)　 が線形従属であることから 証明できます。
[l], [m], [n] が川の字のように並ぶ三直線のときは次の定理を意味します。
　　　　「双曲平面上にどの二本も交わらない三直線 L, M, N があるとき、
　　　　　L と M の両方に直交する直線と N との交点、
　　　　　M と N の両方に直交する直線と L との交点、
　　　　　N と L の両方に直交する直線と M との交点は一直線上にある。」
次のデータで試して下さい。
1x + 0.2y + 0.1(x2+y2+1)
-1x + 0.1y + 0.2(x2+y2+1)
1x + 0y + 0.3(x2+y2+1)

双曲平面上の三角形の外心
li = aix + biy + ci(x2+y2+1), 　　ai2 + bi2 - 4ci2 = -1, 　　ci > 0 　　(i = 1, 2, 3)
のとき、[l1 + l2]　と　 [l1 - l2]　 はそれぞれ P線分　[l1][l2]　 の中点と垂直二等分線です。
明らかに、 l1 - l2,　 l2 - l3,　 l3 - l1　 は線形従属ですから、
双曲平面上の三角形の 三辺の垂直二等分線は一点で交わるか三本のいずれにも直交する 直線があることがわかります。

双曲平面上の三角形の重心
(l1 + l2) * l3,　 (l2 + l3) * l1,　 (l3 + l1) * l2　 も明らかに線形従属ですから、
双曲平面上の三角形の三本の中線も一点で交わることがわかります。

双曲平面上の二次曲線
P直線の定義式が x, y, x2+y2+1 の一次結合ですから、
二次P曲線を x, y, x2+y2+1 の斉次二次式の零点と定義するのは妥当と思われます。
普通の平面の二次曲線は円、楕円、放物線、双曲線、二直線ですが、
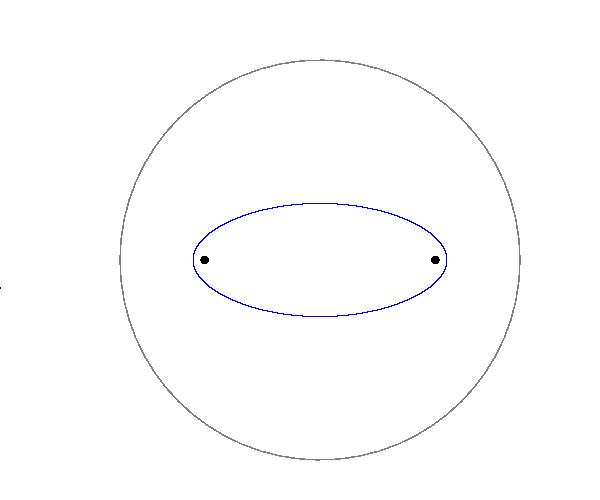
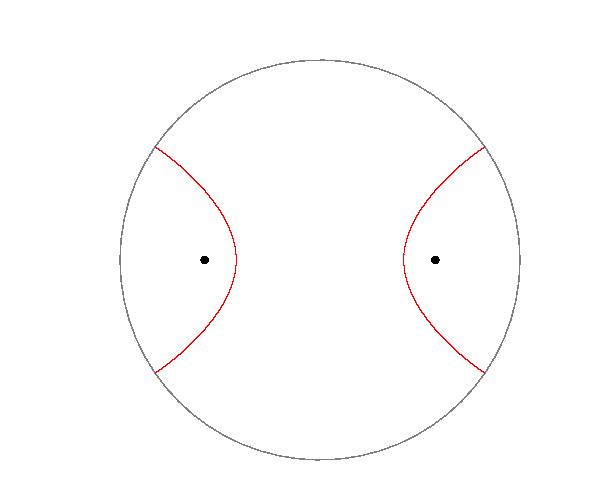
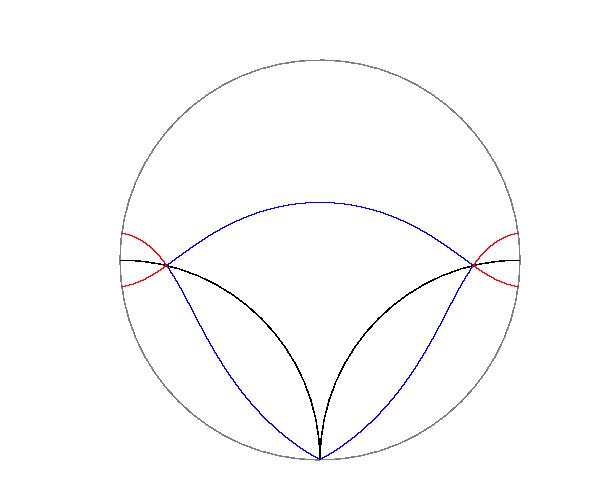
双曲平面でも、2P点からの距離の和(下左図の青い線)または差(下右図の赤い線)が一定の点の軌跡は二次P曲線です。

さらに、2P直線からの距離の和または差が一定の点の軌跡(下左図、中央図)と
1P点と1P直線からの距離の和または差が一定の点の軌跡(下右図)も二次P曲線です。
これらは、双曲平面に特有の二次曲線です。


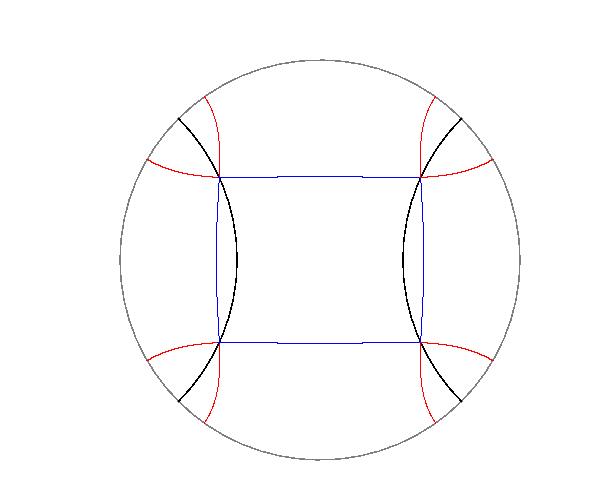
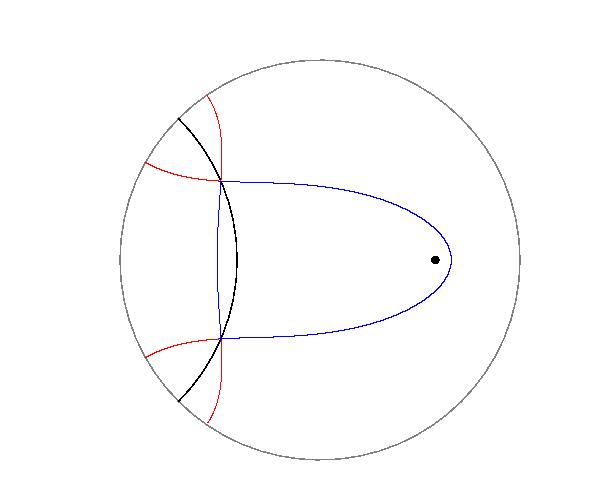
円(1P点から等距離にある点の軌跡)と 1P直線から等距離にある点の軌跡も二次P曲線です。
また、双曲平面上でもパスカルの定理が成り立ちます。


双曲平面上の幾何図形を描くプログラム

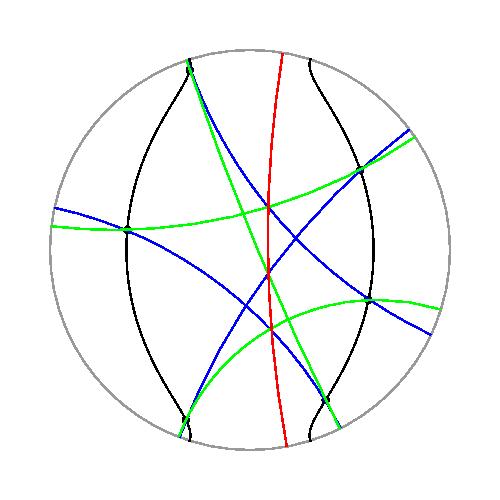
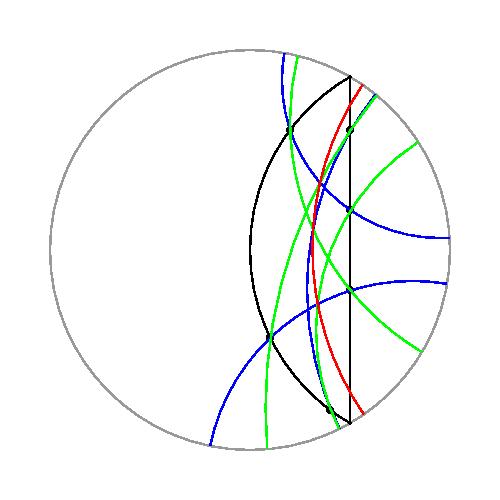
自分で双曲平面上の幾何図形を描きたいときは、 ここから、 hbg.tgz をダウンロードし、
terminal 上で次の二行を実行して下さい。
tar　-xvzf　hbg.tgz
make
次に、以下のように実行して見て下さい。 (drawg を既にダウンロード済みならば、(　) の中を実行して下さい。)
./ext_pro < 2v0.dat　　　　(./ext_pro < 2v0.dat | drawg -s200)
./orthoc < 3v0.dat　　　　(./orthoc < 3v0.dat | drawg -s200)
ソースファイル　ext_pro.cpp　orthoc.cpp　circumc.cpp と Makefile を見てもらえば、
ヘッダファイル hbg.h をインクルードし、 コンパイル時に util.o をリンクすることにより、
プログラムが簡単に書けるようになっていることがわかると思います。