Geometry on the hyperbolic plane

In the hyperbolic plane, the sum of the interior angles of any triangle is smaller than 180^○ (see the lower left figure).

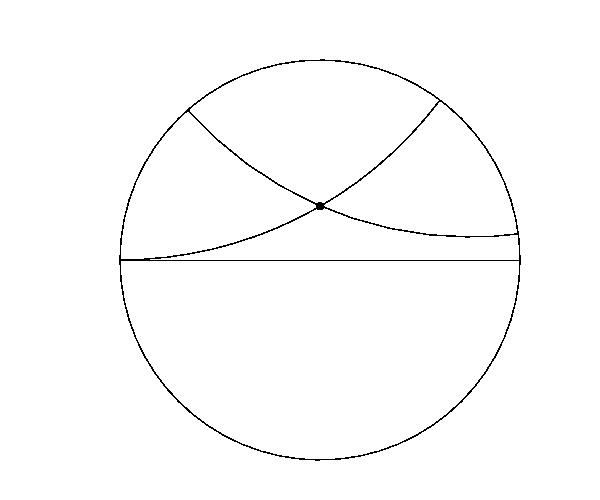
Let l be a line on the hyperbolic plane and let P be a point not on l.
Then there are many lines passing P and not intersecting with l (see the upper right figure).

If two lines does not intersect, then there exists only one line which intersects the two lines at right angle.
We do not distinguish lines and points on the hyperbolic plane, and call them objects.
Let a and b be objects. We denote by ab the object determined by a and b.
When a and b are points, ab is the line passing a and b.
When a and b are lines, ab is the intersection point of a and b, or the line intersecting a and b at right angle.
When a is a point and b is a line, ab is the line passing a and intersecting b at right angle.
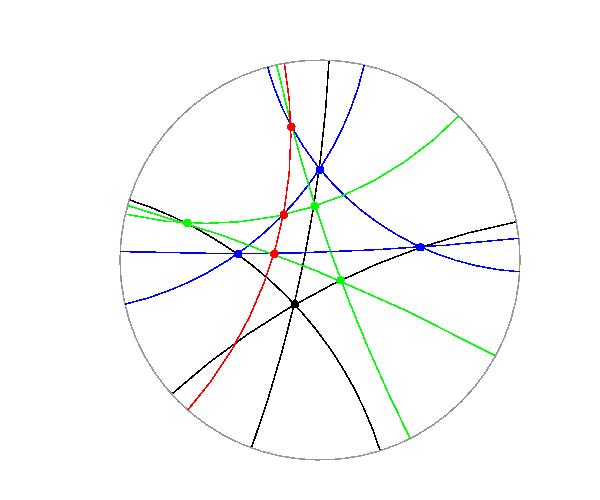
(See the figure bellow.
You can move two points a and b using mouse and
if you pull the points out of the hyperbolic plane, then it change to a line.)

We say that three objects a, b and c are dependent, if ab = bc = ca.
For example, when a, b and c are points, they are dependent if and only if they are on a line.

Desargues theorem holds also in the hyperbolic plane.
Using the above notations, Desargues theorem is expressed as follows:
"Let a, b, c, a', b', c' be objects.
If aa', bb' and cc' are dependent, then (bc)(b'c'), (ca)(c'a') and (ab)(a'b') are dependent."

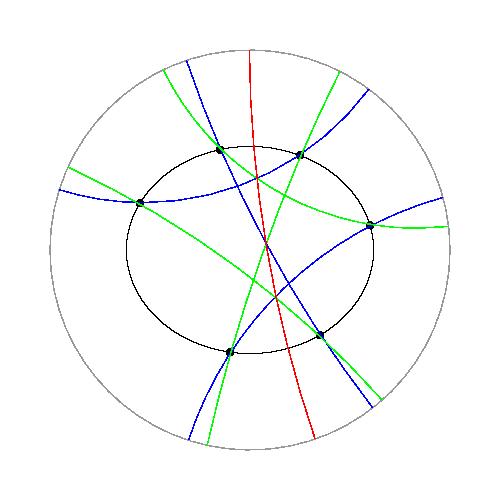
The upper left figure shows the case a, b, c, a', b', c' are all points.
The upper right figure shows the case a, b, c are points and a', b', c' are lines.

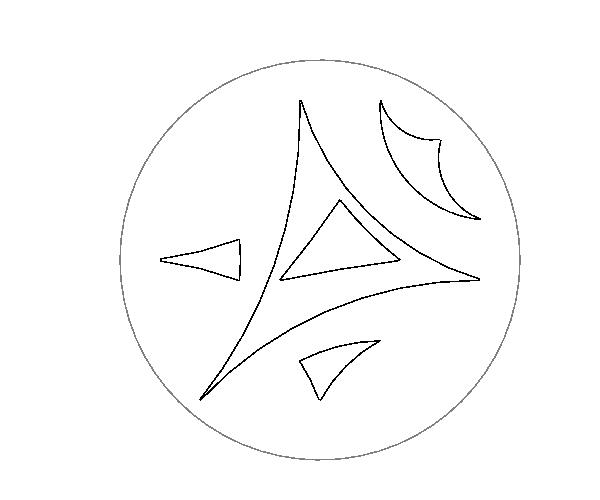
Pascal theorem also holds (See the figures below).

You can move six points on the above circle using mouse.