1. パスカルの定理

2. 拡張されたパスカルの定理
福原満洲雄著 『射影幾何』 実教出版株式会社
p 191 定理 6.2 参照

n本の直線 l₁, ..., l_n と n本の直線 m₁, ..., m_n の n² 個の交点 l_im_j のうち 2n 個が同一円周上にあれば、
残りの n(n - 2)個は n-2 次曲線上にあります。 n = 3 の場合が元のパスカルの定理です。

n = 4 の場合
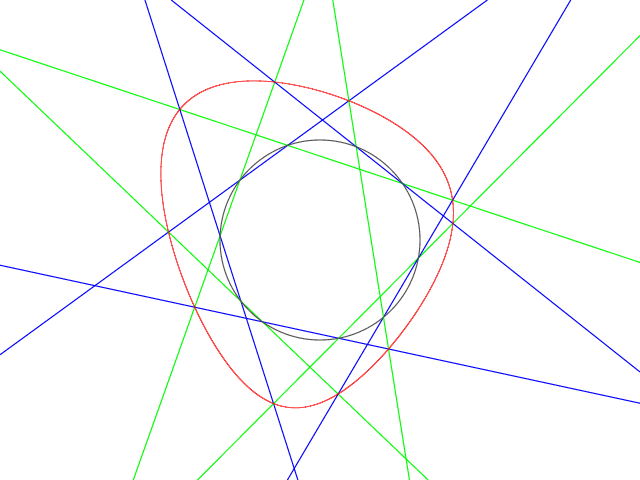
八角形が円に内接しているとき、 八角形の辺に青、緑、青、緑 ... と色を付ければ、 青と緑の交点で円の上にないものが8個あります。
注:平面上に勝手に8個の点を与えたとき、 その8個の点を通る二次曲線は存在しません。
(円上の点は動かせます。)


n = 5 の場合

3. 三つ巴のパスカルの定理

パスカルの定理の結論の一直線上にあるというときの 直線をパスカル線と呼びます。
下図ではパスカルの定理が３つ重なっていて青色と緑色の線からなる六角形に対するパスカル線が空色, 緑色と赤色の線に対するパスカル線が黄色、赤色と青色の線に対するパスカル線が紫色ですが, この三本のパスカル線が一点で交わっています。

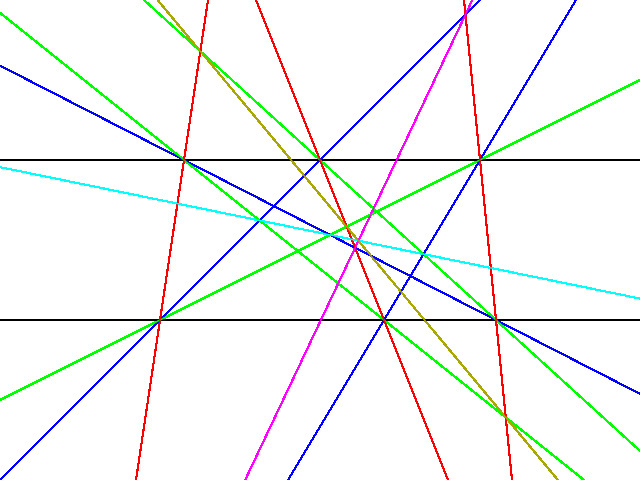
<-ここをクリック
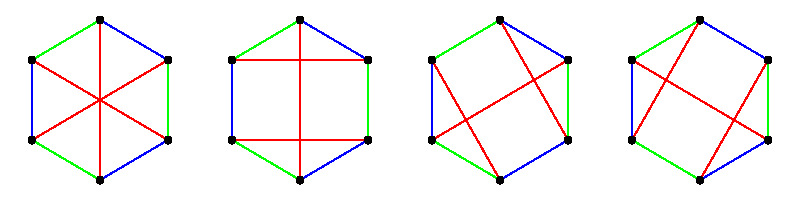
二次曲線上の6点を 下図左のように結んでできる三つの六角形 に対するパスカル線が交わった点はシュタイナー点,
下図右の三つに対するそれらはキルクマン点と呼ばれています。
二次曲線が二直線の場合(上右図)にはシュタイナー点だけになります。

シュタイナー点, キルクマン点についての詳しい説明は 幾何学大辞典 6(ISBN 4837503152) の附録に載っています。
代数的な方法を使えば,シュタイナー点, キルクマン点のいずれの場合も簡単に証明でき, さらには次のようなことも証明できます。

　定理 3.1 n, m を n > m > 0 を満たす整数とする。 二つの n次曲線 S₁, S₂ の n²個の交点のうち, nm個が一つの m次曲線上にあれば,
残りの n(n-m)個は n-m次曲線上にある。
　定理 3.2 n, m を n > m > 0 を満たす整数とする。 S₁, S₂, S₃ は n次曲線で m次曲線上の nm点で交わっているとする。
S_i と S_j に対する定理 3.1 の n-m次曲線を T_6-i-j とすれば, T₁, T₂, T₃ は共点である。

n=3, m=2 で S_i が 3直線の場合がパスカルの定理です。
n=3, m=1 で S_i が 3直線の場合が下左図で,パスカルの定理の逆が３つ重なっています。
n>3, m=2 で S_i が n直線の場合が 2.のパスカルの定理の拡張です。 下右図は n=4 の場合です(円上の点は動かせます)。

4. パスカル線とキルクマン点

E. Loid:"Symmetry and Pattern in Projective Geometry"(Springer)の96ページに
The Kirkman points and Pascal lines form a configulation (60₃), which consists of three separate Dezargues' (10₃) configulations.
と書いてありますが, three は six が正しいと思われます。 この記述の後半部分について図を用いて説明します。
二次曲線上の 6点(どの 3点も一直線上にない)のすべてを通る 3直線は 15通りあります。 それをグラフで表したものが下図の a から o です。


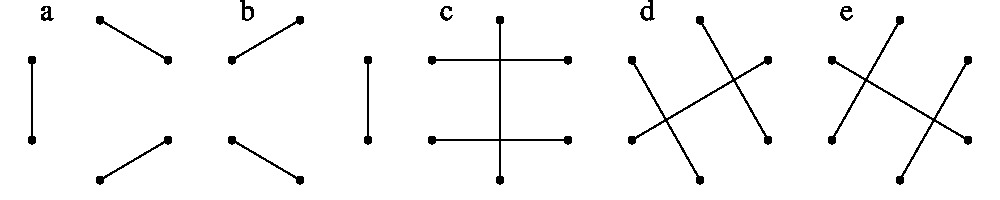
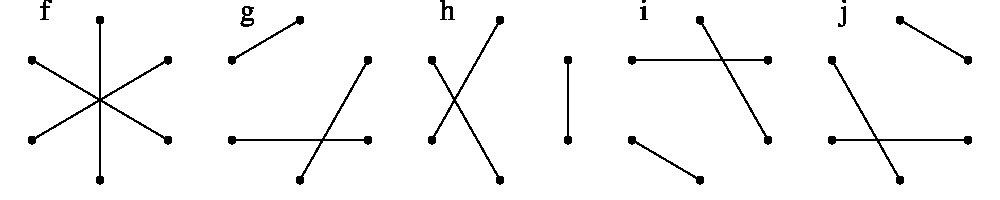
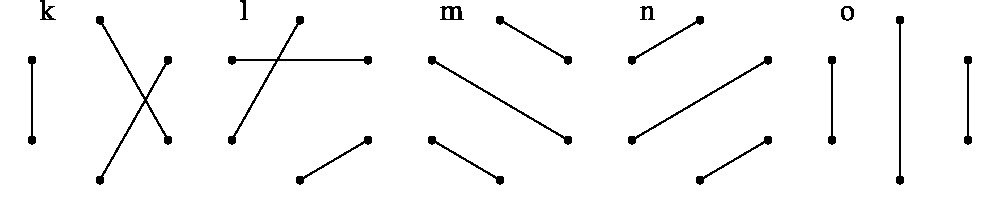
a から o のグラフから同じ辺を共有しない 2つ(例えば a と b)を選べば, 合わせて六角形ができ, 一つのパスカル線が対応します。
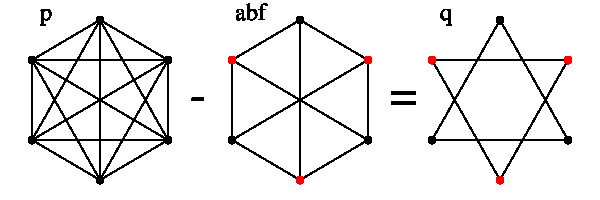
また, 同じ辺を共有しない 3つを選べば, それらを合わせて完全二部グラフになるとき(例えば abf)はシュタイナー点,
そうでないとき(例えば abc)はキルクマン点が対応します。
以下の6つのグループを考えます。
I : {a, b, c, d, e}, II : {a, f, g, h, i}, III : {b, f, j, k, l}, IV : {c, h, k, m, n}, V : {d, g, l, m, o}, VI : {e, i, j, n, o}
これらのグループには以下の特徴があります。
　1. a から o のどの文字も二つのグループに属す。 逆に, どの二つのグループにも共通の文字が一つだけある。
　2. 各グループ内の 5つのグラフには共通の辺がなく, 全部合わせると完全グラフになる。
　3. 同じグループに属しない 2つのグラフには共通の辺がある。
特徴 2. より, 各グループから 2つのグラフを選べば, パスカル線が対応し,
3つのグラフを選べば, キルクマン点が対応します。
3つのグラフを合わせて完全二部グラフにならないことは上右図からわかります
(q のグラフからどの 3本の辺を選んでも, 辺が 2本出ている頂点ができてしまうから, a から o のどの二つのグラフをあわせても q にはならない)。
したがって, 一つのグループから 10本のパスカル線と10個のキルクマン点が得られます。
さらには, 一本のパスカル線上には 3個のキルクマン点があることもわかります
(例えば, ab に対応するパスカル線上には abc, abd, abe に対応するキルクマン点)。

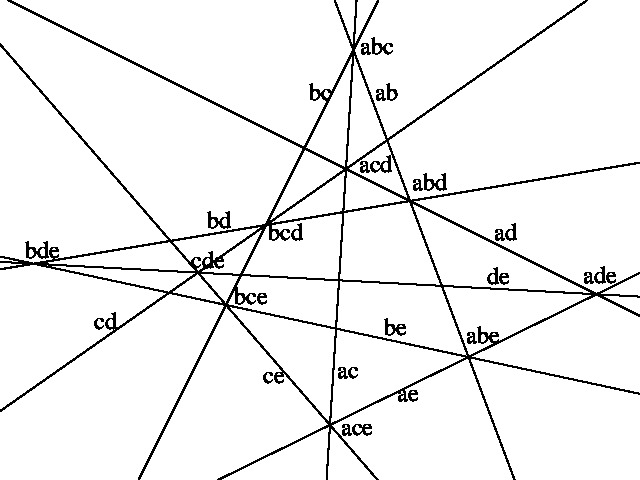
同じ辺を共有しない 2つのグラフに対して合わせて完全二部グラフとなるグラフは 一つだけである(例えば, ab に対しては f)ことから,
一本のパスカル線上のシュタイナー点は一つだけであることがわかります。
また, 上述したように合わせて完全二部グラフとなる 3つのグラフは一つのグループに属しないことから,
シュタイナー点で交わる 3本のパスカル線は異なるグループに属すこともわかります。
例えば, abf に対して ab, af, bf はそれぞれ I, II, III に属す。