リサージュ曲線の回転数
x = cos mt, y = sin nt (0 < t < 2pi)
m / (m, n) が奇数のときは滑らかな曲線になります ((m, n) は m と n の最大公約数です)。
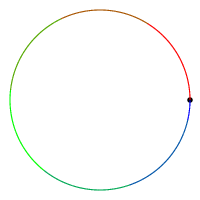
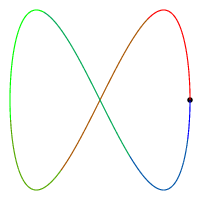
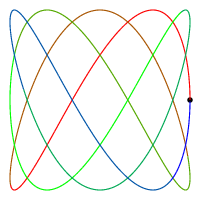
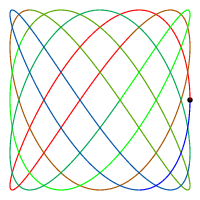
| m = 1, n = 1 | m = 1, n = 2 | m = 3, n = 5 | m = 5, n = 7 | |
 |
 |
 |
 |
|
| 回転数 | 1 | 0 | -1 | 1 |
平面閉曲線の回転数とは一言でいえば、 曲線に向きを付けて考え、 平面上を反時計間回りに何回転しているかを表す整数です。 上の例では色が赤、 緑、 青と変わる向きで考えています。
正確な定義と詳しい説明については 小林昭七著「曲線と曲面の微分幾何」裳華房 p16-19 を参照して下さい。
(m, n) > 1 のときは m' = m /(m, n), n' = n / (m, n) とすれば、
x = cos mt, y = sin nt で表される閉曲線の回転数は
x = cos m't, y = sin n't で表される閉曲線のそれの (m, n) 倍となることはすぐにわかります。
m が奇数で n が偶数のとき、回転数は 0 となります(この証明は簡単です)。
定理
m と n は互いに素な正整数であり、
m を 4 で割った余りが 1 (3) で、 n が奇数のとき、
x = cos mt, y = sin nt (0 < t < 2pi)
で表される閉曲線の回転数は 1 (-1) である。
注 : 上の定理は前澤(旧姓 嶺岸)祐子さんと私で証明した定理です。
微分幾何学の専門家何人かに聞いてみましたが、 この定理は既にどこかに書かれているというような答えは聞かれませんでした。
この定理が載っている本または雑誌をご存知の方がおられましたら お知らせ下されば有難いです。
x = cos( t), y = sin( t)で表される曲線
と連続的に変形して回転数が 1 または -1 であることをアニメーションにより示します。