Ponceletの閉形定理

Darbouxの定理

Q を円, C を n 次曲線とする。
Q の相異なる n+1 本の接線 l_0, l_1, ..., l_n で
交点 l_il_j がすべて C 上にあるものが存在すれば、
Q の任意の接線 m_0 に対して
Q の n 本の接線 m_1, ..., m_n で
交点 m_im_j がすべて C 上にあるものが存在する。
ただし、m_i = m_j となる場合もあり、 このとき m_im_j は m_i と Q の接点とする。

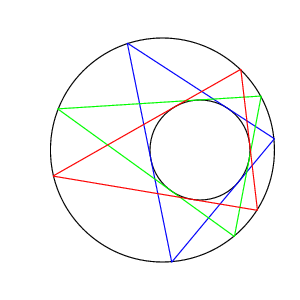
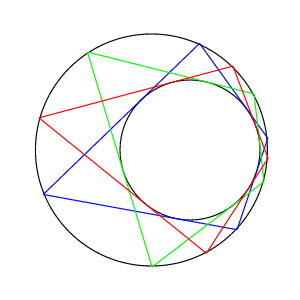
下図は n = 3 の場合である。


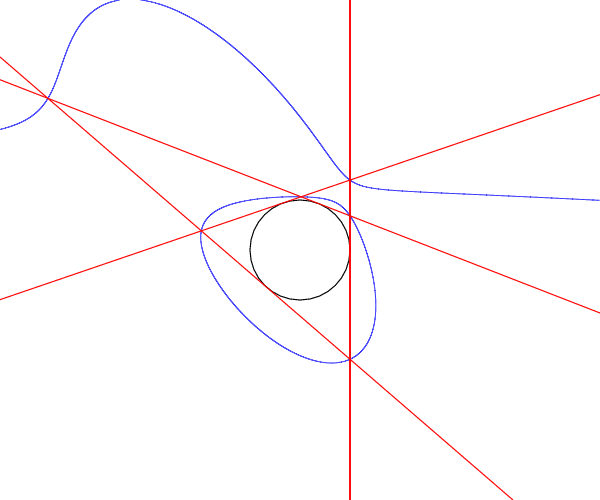
Q1, Q2 を相異なる二次曲線とし、n を 4 以上の整数とする。
Q1 の n 本の相異なる接線 l_1, l_2, ... , l_n で n 個の交点 l_1l_2, ..., l_n-1l_n, l_nl_1 が Q2 上にあるものが存在すれば、 Poncelet の定理より l_1, l_2, ... , l_n と異なる Q1 の接線 m_1 に対して Q1 の接線 m_2, ..., m_n で n 個の交点 m_1m_2, ..., m_n-1m_n, m_nm_1 が Q2 上にあるものが存在する。
このとき、 0 でない任意の定数 c に対して
l_1l_2...l_n + cm_1m_2...m_n = 0
で定義される n 次曲線 C は n^2 個の交点 l_im_j を通る。
Q1 の任意の接線 l'_1 に対して Q1 の接線
l'_2, ..., l'_n, m'_1, m'_2, ..., m'_n
で 2n 個の交点
l'_1l'_2, ..., l'_n-1l'_n, l'_nl'_1, m'_1m'_2, ..., m'_n-1m'_n, m'_nm'_1
が Q2 上にあり、 n^2 個の交点 l'_im'_j が C 上にあるものが存在する。