双曲平面という世界では、180○より小さくなります。
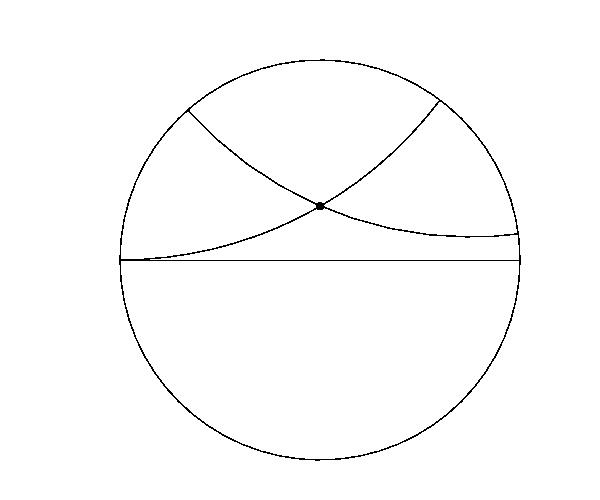
この世界はポアンカレ円盤という鏡(下左図)を通して覗くことができます。
双曲平面の直線は円盤の直径か境界に直交する円の円盤内に含まれる円弧のように見えます。
下右図からわかるように、三角形は大きくなるほど、 内角の和は 0○ に近づきます。
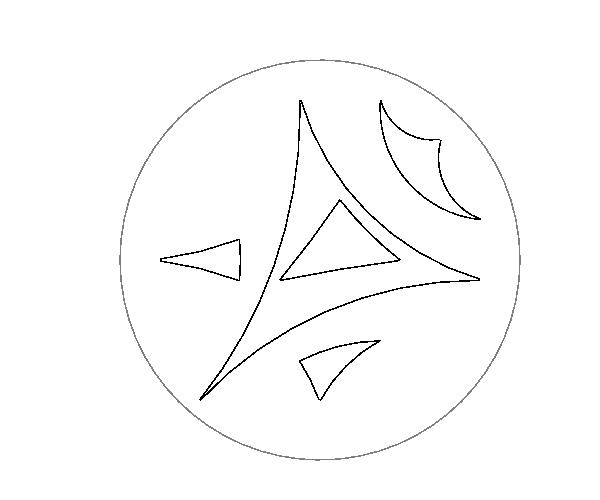
また、円盤の境界に近づくほど、同じ大きさのものでも小さく見えます。
下左図と右図はそれぞれ四角形と五角形で双曲平面を敷き詰めていますが、
いずれも同じ形、同じ大きさです。
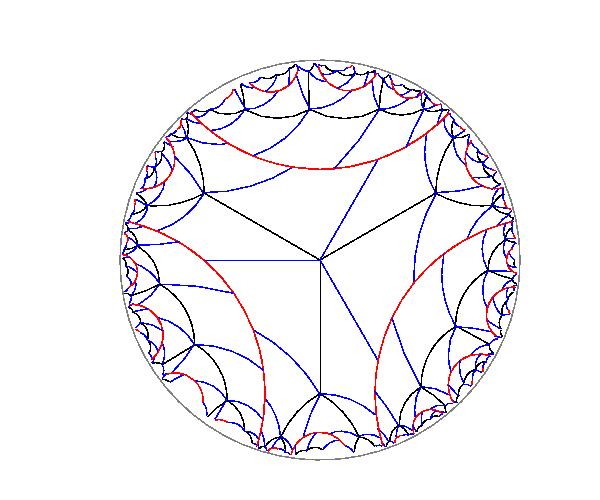
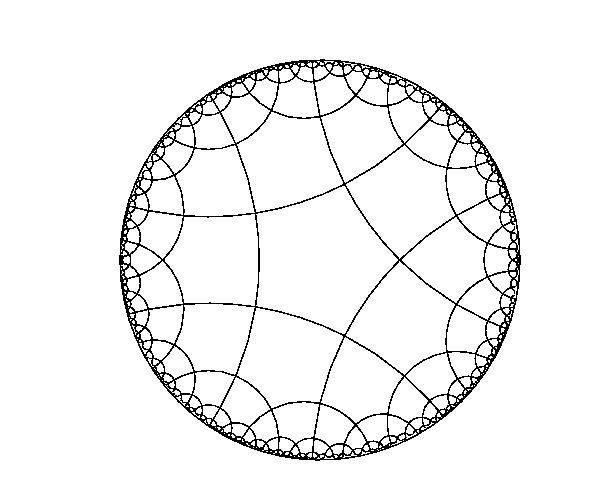
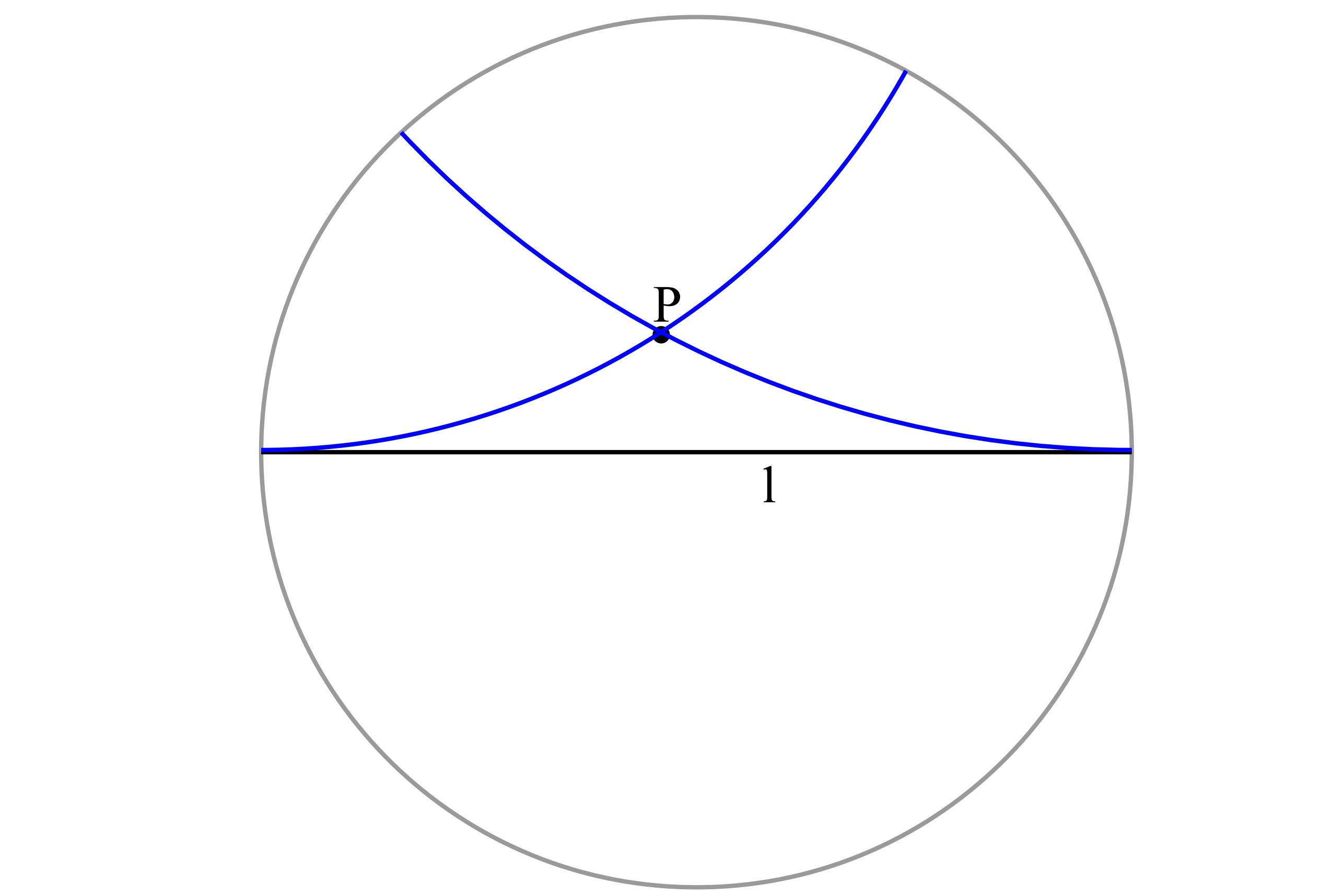
普通の平面では直線 l とその上にない点 P があるとき、
P を通って l と交わらない直線は唯一つですが、 双曲平面では無限にあります。
その中でも下左図の二本の青い直線を黒い直線 l と極限平行であるといい、
それ以外の l と交わらない直線を l と平行であるといいます。
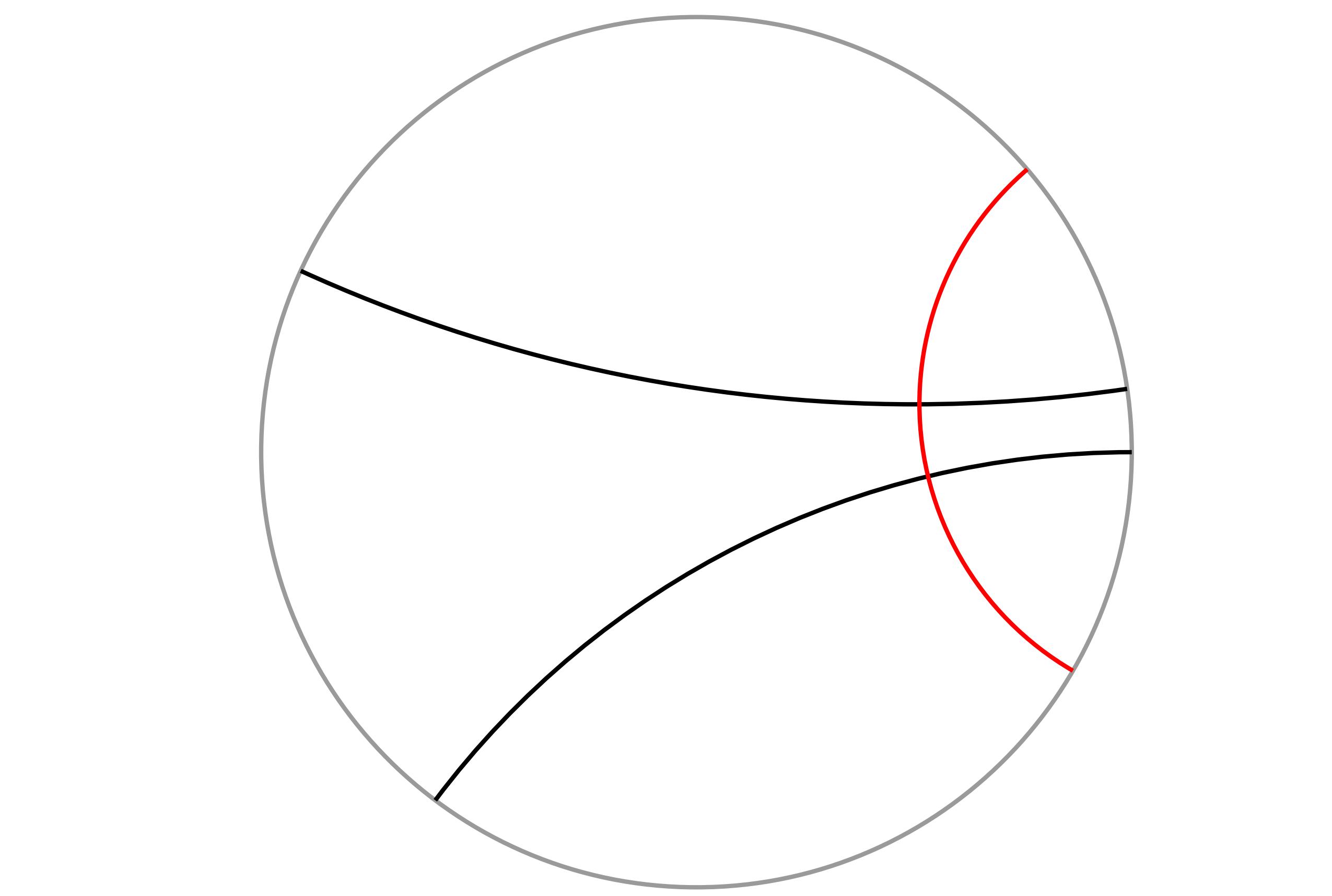
また、二直線が平行のとき、下右図の赤い直線のように、
二直線の両方に直交する直線が唯一つあります。
方巾の定理や 「外心、垂心、重心が一直線上にある。」
のように双曲平面上では成り立たないものもありますが、
以下のような射影幾何的な定理は成り立ちます。
下図は双曲平面上でデザルグの定理を考えた図です。
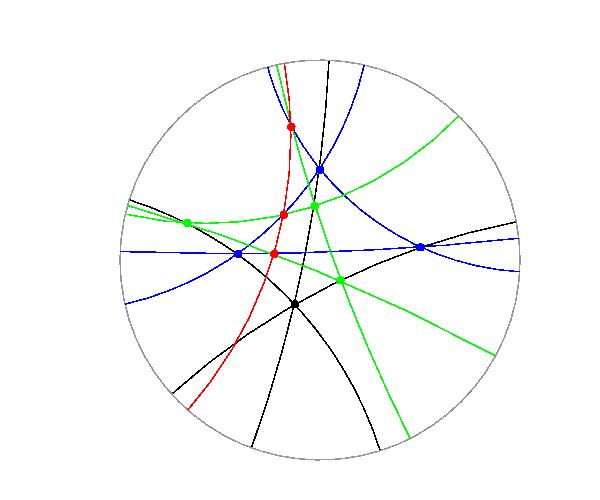

下図は双曲平面上でパスカルの定理を考えた図です。
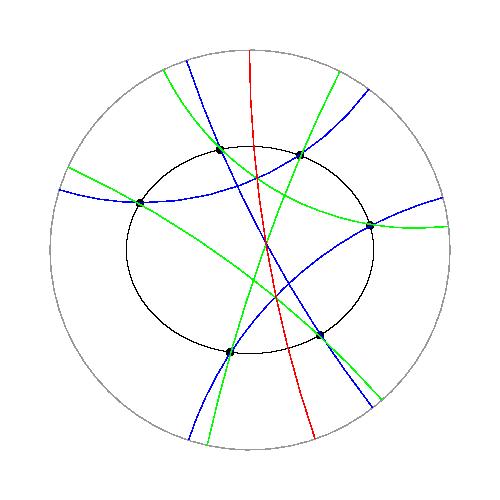
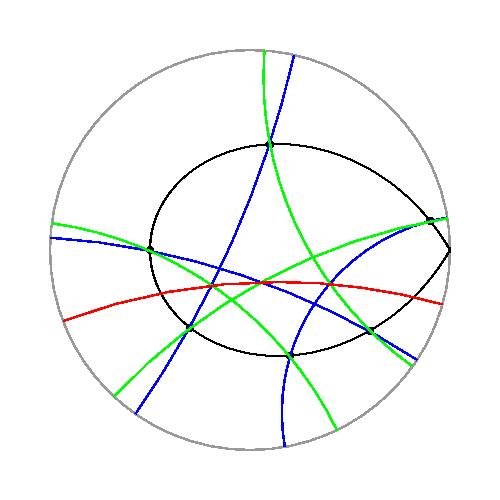
下図は双曲平面上のPonceletの閉形定理の図です。
ここをクリックすればアニメーションで見れます。
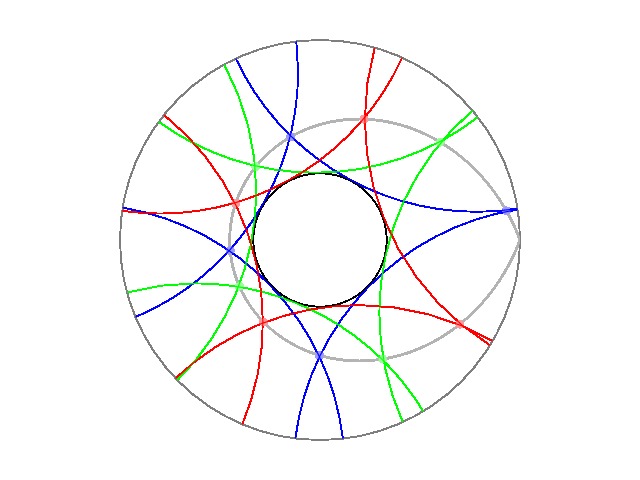
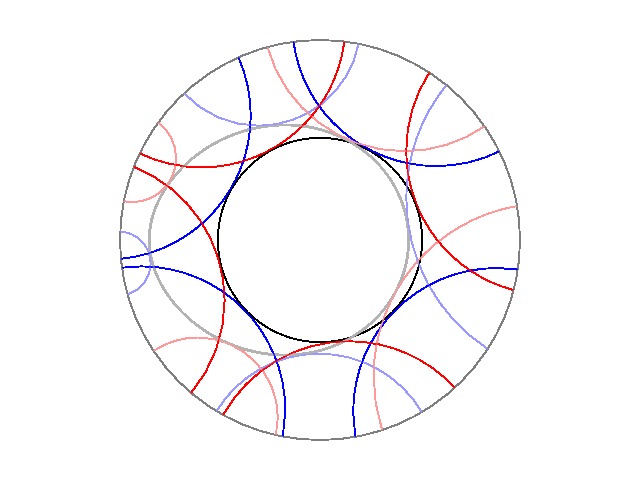
双曲平面上では点と直線を同列に扱うべき
双曲平面上でデザルグの定理やパスカルの定理を考えたとき、
2直線の交点という所で交わらないときにどう考えるかが問題となります。
ある本には次のように書かれています(一部、言葉遣いを変えてあります)。
また、直線 BC と直線 B'C', 直線 CA と直線 C'A', 直線 AB と直線 A'B'
が異なり、それぞれ A'', B'', C'' で交わるとする。
このとき、三つの直線 AA', BB', CC' が一点で交わるか、平行ならば
A'', B'', C'' は一直線上にあり、逆の命題も成り立つ。」
ここで、BC と B'C' が交わらないときにはどうなるのかという疑問が浮かびますが、
上で書いたように、双曲平面では2直線が交わらず、極限平行でもないときには
2直線の両方に直交する直線が唯一つあります。
このように、双曲平面上では極限平行でない2直線に対して
点または直線が唯一つ決まりますので、
また、結論の「3点が一直線上にある。」 の代わりに三つの対象が
2点と1直線 : 2点を通る直線が1直線と直交する
1点と2直線 : 2直線の両方に直交する直線が1点を通る
3直線 : 一点で交わるかいずれにも直交する直線がある
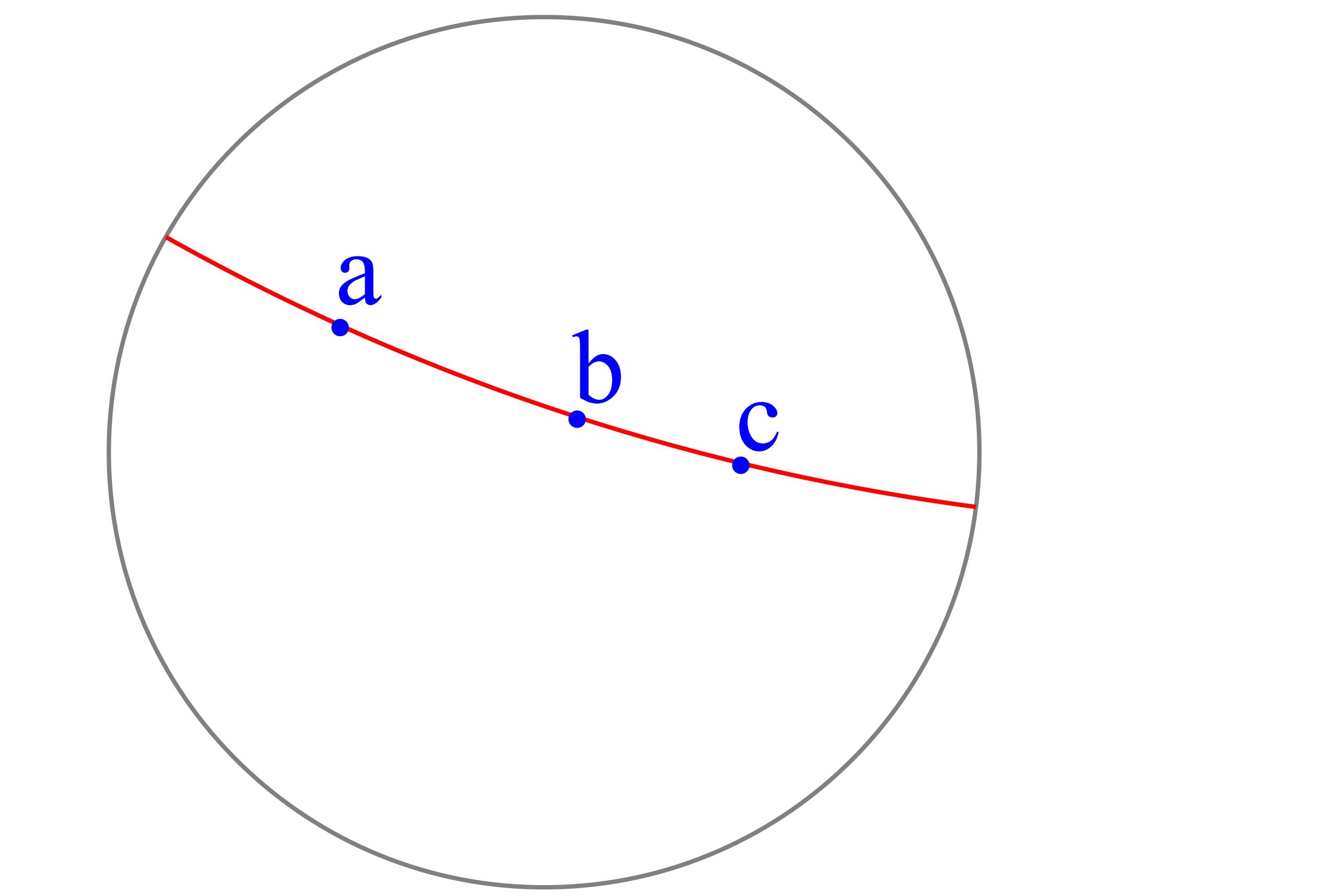
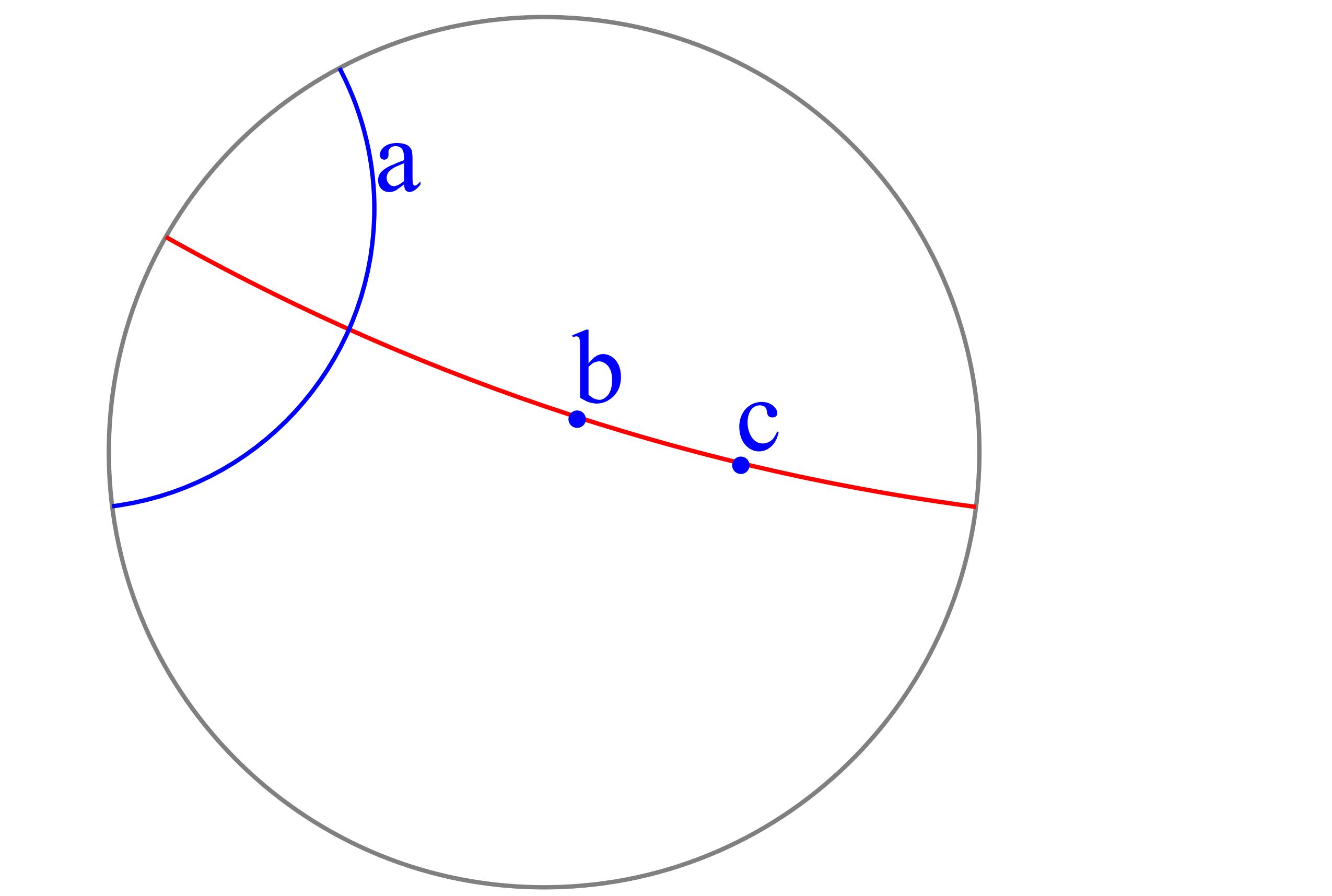
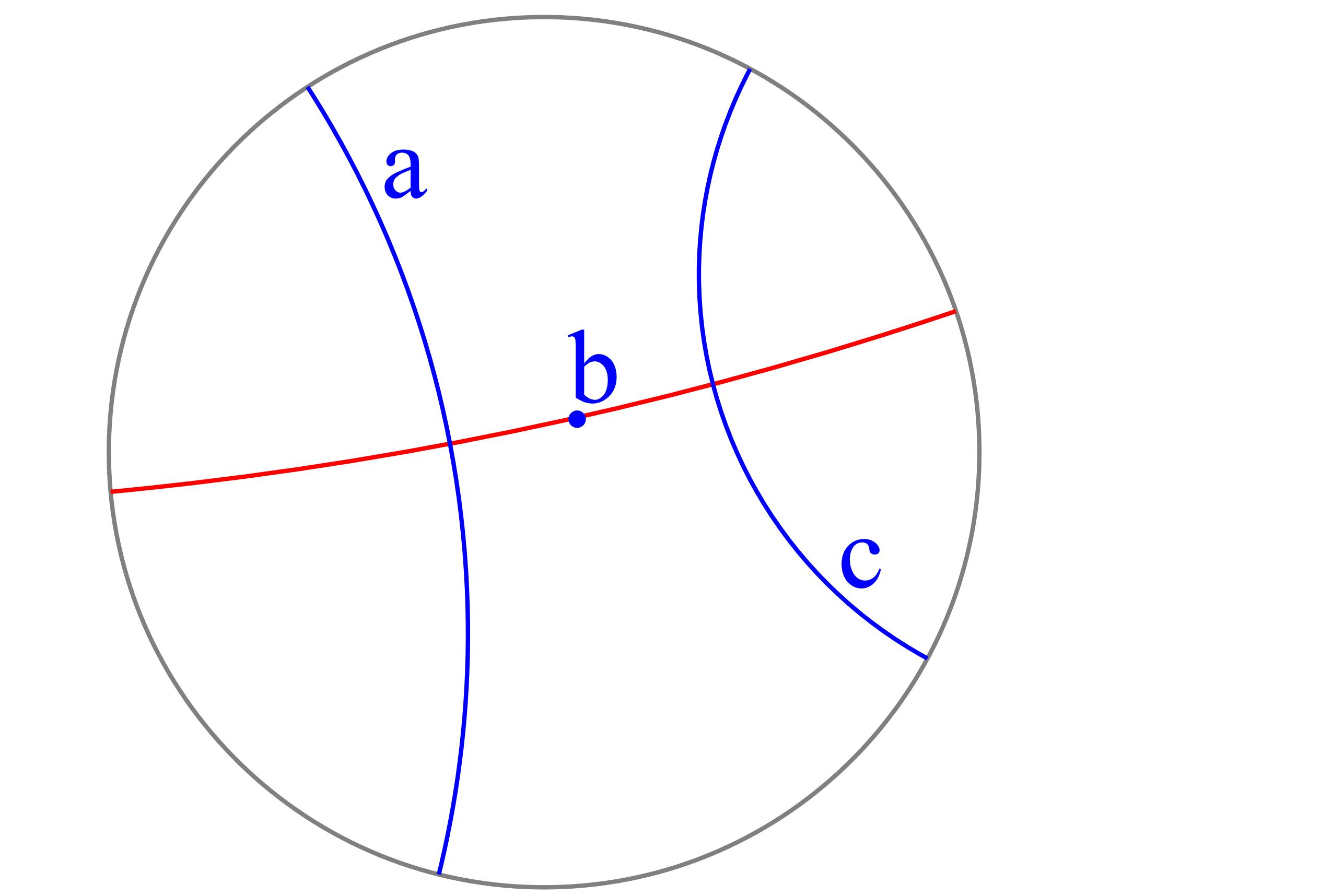
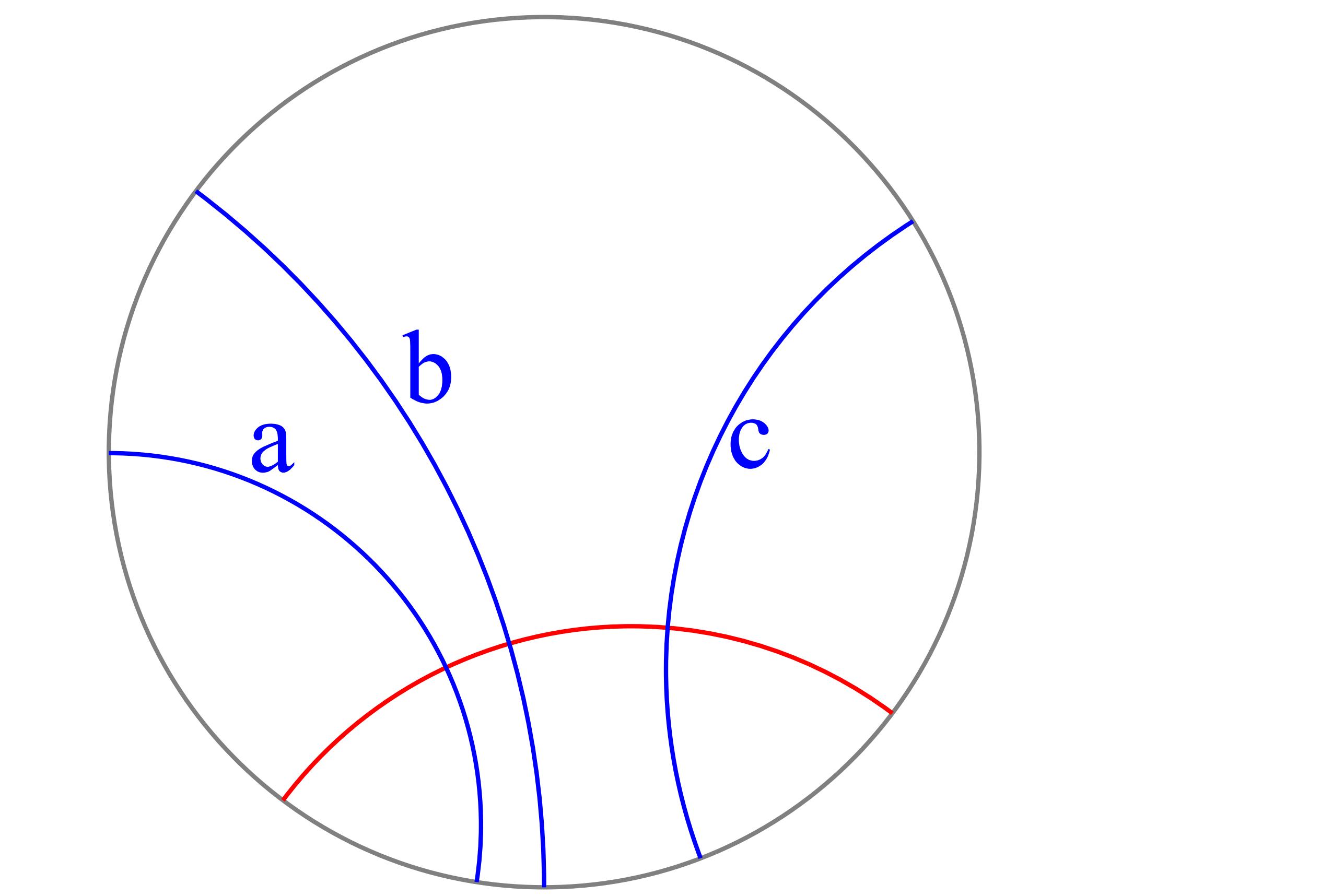
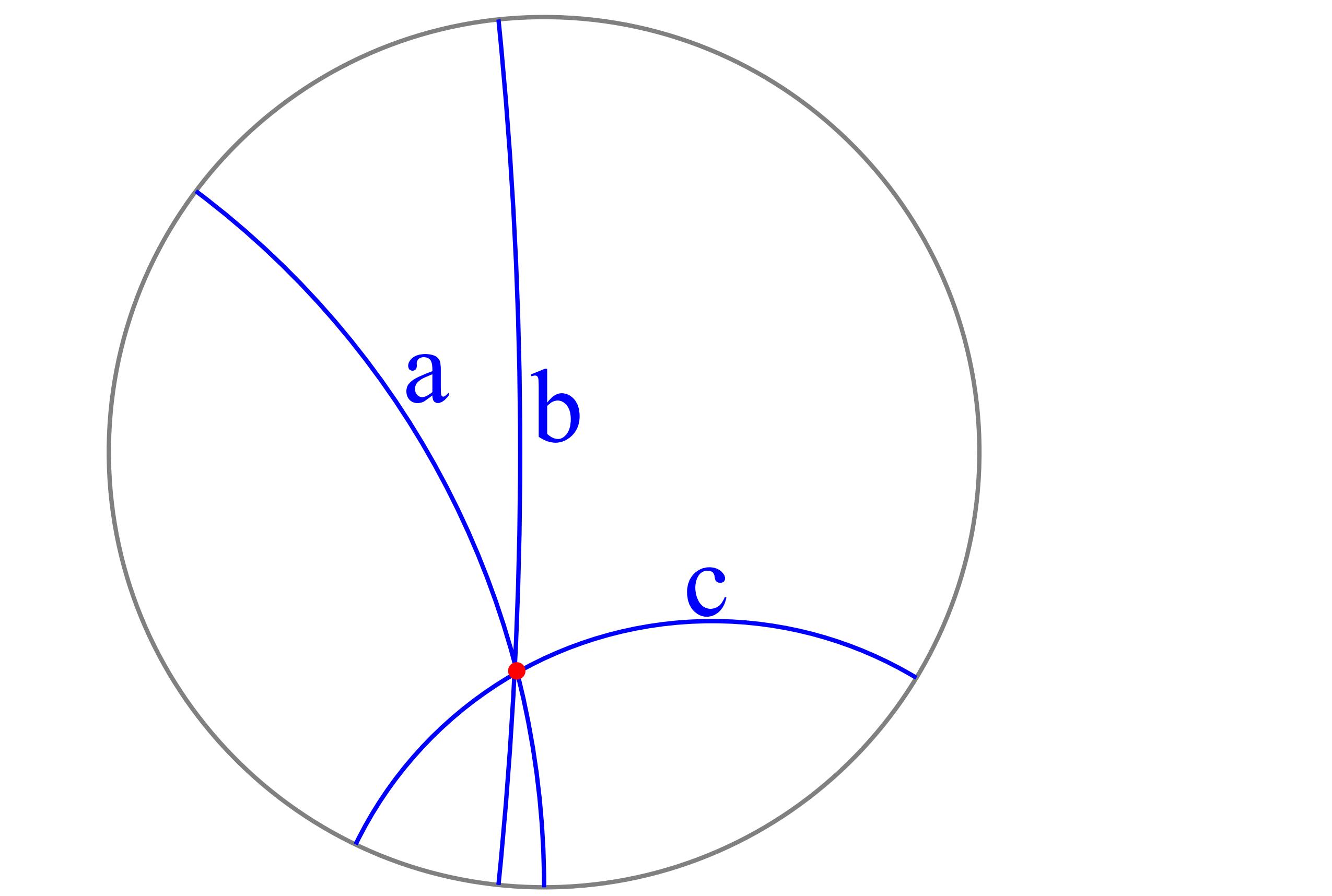
また、二つの対象
1点と1直線 : 1点を通り1直線に直交する直線
2直線 : 2直線の交点または両方に直交する直線
上図で a を青色、b を緑色、ab を赤色で表しています。
a と b はマウス(タブレットならば指)で動かすことができます。
円の外に出せば、直線に変わります。
この記号を使えば、
ab = bc = ca が成り立つこと
また、双曲平面上のデザルグの定理 は次のように表すことができます。
を満たす双曲平面上の対象とするとき、
aa', bb' cc' が従属しているならば
(bc)(b'c'), (ca)(c'a'), (ab)(a'b') も従属している。」
a, b, c が点で、 a', b', c' が直線でどの二つも交わるときは次の定理を意味します。
A から B'C' に下ろした垂線、
B から C'A' に下ろした垂線、
C から A'B' に下ろした垂線が一点で交われば、
A' から BC に下ろした垂線、
B' から CA に下ろした垂線、
C' から AB に下ろした垂線も一点で交わる。」
同様に、ユークリッド平面上の1つの定理から
双曲平面上のさまざまな定理が得られることがあります。
その例が以下のリンク先で見られますのでクリックして試して下さい。
双曲平面上の三角形の垂心
双曲平面上の一つの定理
((al)l)(bc), ((bl)l)(ca), ((cl)l)(ab) は従属している。」
双曲平面上の一つの定理 その二
b, c, p が従属し、c, a, q が従属し、a, b, r が従属し、
さらに ap, bq, cr が従属していれば、
(bc)(qr), (ca)(rp), (ab)(pq) も従属している。」
双曲平面上の一つの定理 その三
b, c, p が従属し、c, a, q が従属し、a, b, r が従属し、
さらに p, q, r が従属していれば、
((ap)(bq))c, ((bq)(cr))a, ((cr)(ap))b も従属している。」